使用方法

1. 複素透過率（パワー透過率と位相）であるwave を作成する。周波数情報は change wave scaling であらかじめwave の中に取り込んでおく。また位相スペクトルは2πの補正を手動で行っておく。
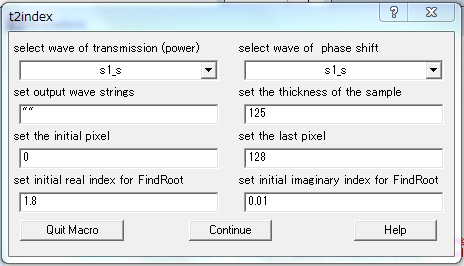
2. マクロ t2index を起動すると以下のような入力項目が出てくる。 "select wave of transmission (power)"および "select wave of phase shift"にはそれぞれ対応するwave を選ぶ。 "set output wave strings"では出力するwave の文字列を入力する。出力されるwave の名前は "_n"と"_k"が自動的に追加される
3. "set the thickness of the sample"では試料の厚さをum で入力する。
4. "set the initial pixel"および"set the last pixel"では計算する周波数範囲を pixel で入力する。ノイズの大きな領域まで計算させるとプログラムが止まる可能性がある。
5. "set initial index for FindRoot"ではFindRoots機能を実行させるための屈折率の初期値（実部と虚部） を入力する。

カスタマイズ、その他

1. FindRoots 機能では複素屈折率の初期値を入力する必要があります。 １つの複素透過率から得られた屈折率の値を次の計算における初期値とする場合には 最後の方にある
   in_n=W_Root[0]
   in_k=W_Root[1]
   を有効にしてください
2. 位相の取り扱いが複素屈折率の計算結果に大きな影響を与えます。single pass の場合では データに2Pi の飛びがあると正しい屈折率が得られませんので、位相データを 直接修正してください。また多重反射を考慮する場合には計算において位相範囲は -PiからPiとなっています。したがって初期値によって収束する屈折率の扱いが異なります。 まずはsingle pass で屈折率の値を計算した後で多重反射での解析を行ってください。
3. 本プログラムでは計算領域以外のピクセルはNaNを返します。既存の計算結果に 新たにあるピクセル領域での結果を追加する場合には、
   Duplicate/O $ww1 $ww5, $ww6
   $ww5=NaN
   $ww6=NaN
   　を"//"で無効にしてください
4. 多重反射の解析のための式には基板の屈折率（変数 n_s=cmplx(1,0)）を変えることができます。 振幅および位相の２つの関数mytds_m1　およびmytds_m2の２つがありますので、両方の関数における 屈折率の値を変えてください。

/////////////////////////////////////////////////
// This procedure is for evaluation of refractive index 
// from complex transmission measured by THz TDS
//    created by M. Nagai on Jan., 2012, 
/////////////////////////////////////////////////


Function mytds_s1(w, x1, x2)	// analysis with assumption of single pass
	Wave w           //w[0]=thickness um  w[1]=freq THz  w[2]=T  w[3]=phase
	Variable x1,x2  // index (real and imaginary)
	Variable/C x    //complex index
	Variable AA,BB
	AA=300/(2*Pi*w[0]*w[1])
	x=cmplx(x1,x2)
	BB=w[3]-imag(r2polar(x/(x+1)^2))
	return 1-x1+AA*BB
End

Function mytds_s2(w, x1, x2)	// analysis with assumption of single pass
	Wave w           //w[0]=thickness um  w[1]=freq THz  w[2]=T  w[3]=phase
	Variable x1,x2  // index (real and imaginary)
	Variable/C x    //complex index
	Variable AA,BB
	AA=300/(2*Pi*w[0]*w[1])
	x=cmplx(x1,x2)
	BB=cabs(sqrt(w[2])/4/x*(x+1)^2)
	return x2+AA*ln(BB)
End


Function mytds_m1(w, x1, x2)     // analysis with assumption of multi-reflection
	Wave w  //w[0]=thickness um  w[1]=freq THz  w[2]=T  w[3]=phase
	Variable x1,x2 // index (real and imaginary)
	Variable x=w[1]
	Variable t=w[0]					//thickness
	Variable/C n_f=cmplx(x1,x2)
	Variable/C n_s=cmplx(1,0)		// index of the substrate
	Variable/C r12,r23,t12,t23,prop_f, prop_d
	Variable/C ttt, deno, numer, t12t
	r12=(n_f-1)/(n_f+1)
	r23=(n_s-n_f)/(n_s+n_f)
	t12=2/(n_f+1)
	t23=2*n_f/(n_s+n_f)
	t12t=2/(n_s+1)
	prop_f=2*Pi*t*x/300*n_f*cmplx(0,1)
	prop_d=2*Pi*t*x/300*(n_f-1)*cmplx(0,1)
	numer=t12*t23*exp(prop_d)
	deno=1+r12*r23*exp(2*prop_f)
	ttt=numer/deno/t12t
	return magsqr(ttt)-w[2]
End

Function mytds_m2(w, x1, x2)     // analysis with assumption of multi-reflection
	Wave w  //w[0]=thickness um  w[1]=freq THz  w[2]=T  w[3]=phase
	Variable x1,x2 // index (real and imaginary)
	Variable x=w[1]
	Variable t=w[0]					//thickness
	Variable/C n_f=cmplx(x1,x2)
	Variable/C n_s=cmplx(1,0)		// index of the substrate
	Variable/C r12,r23,t12,t23,prop_f, prop_d
	Variable/C ttt, deno, numer, t12t
	r12=(n_f-1)/(n_f+1)
	r23=(n_s-n_f)/(n_s+n_f)
	t12=2/(n_f+1)
	t23=2*n_f/(n_s+n_f)
	t12t=2/(n_s+1)
	prop_f=2*Pi*t*x/300*n_f*cmplx(0,1)
	prop_d=2*Pi*t*x/300*(n_f-1)*cmplx(0,1)
	numer=t12*t23*exp(prop_d)
	deno=1+r12*r23*exp(2*prop_f)
	ttt=numer/deno/t12t/p2rect(cmplx(1,w[3]))
	return imag(r2polar(ttt))	
End


Macro t2index(ww1,ww2,ww4, thickness,st, fn, in_n, in_k)	
	String ww1,ww2,ww4  //1 trans,  2 phase,  ,  4 output
	Variable st=0,fn=128,  thickness=125
	Variable in_n=1.8, in_k=0.01
	Prompt ww1, "select wave of transmission (power)",popup WaveList("*", ";","")
	Prompt ww2, "select wave of  phase shift",popup WaveList("*", ";","")
	Prompt ww4, "set output wave strings"
	Prompt thickness, "set the thickness of the sample"
	Prompt st, "set the initial pixel"
	Prompt fn, "set the last pixel"
	Prompt in_n, "set initial real index for FindRoot"	
	Prompt in_k, "set initial imaginary index for FindRoot"
	
	String ww5=ww4+"_n", ww6=ww4+"_k", ww3="para"
	Silent 1
	PauseUpDate
	Make/N=4/D/O $ww3
	$ww3[0]=thickness

// if  you evaluate index in limited region, set the following 3 lines invalid
	Duplicate/O $ww1 $ww5, $ww6
	 $ww5=NaN
	 $ww6=NaN
	 
	do
	$ww3[1]=pnt2x($ww1, st)
	if(pnt2x($ww1, st)>0)
		$ww3[2]=$ww1[st]
		$ww3[3]=$ww2[st]
		
//  choose the command (single pass or multi pass)
		FindRoots/X={(in_n),(in_k)}/Q  mytds_s1, $ww3, mytds_s2, $ww3   // single-pass
//		FindRoots/X={(in_n),(in_k)}/Q  mytds_m1, $ww3, mytds_m2, $ww3  //multi-pass

		$ww5[st]=W_Root[0]
		$ww6[st]=W_Root[1]

//	If index is strongly dependent of frequency, set the following two lines valid		
//		in_n=W_Root[0]
//		in_k=W_Root[1]
	endif
	st+=1
	while(st-fn-1)
endmacro